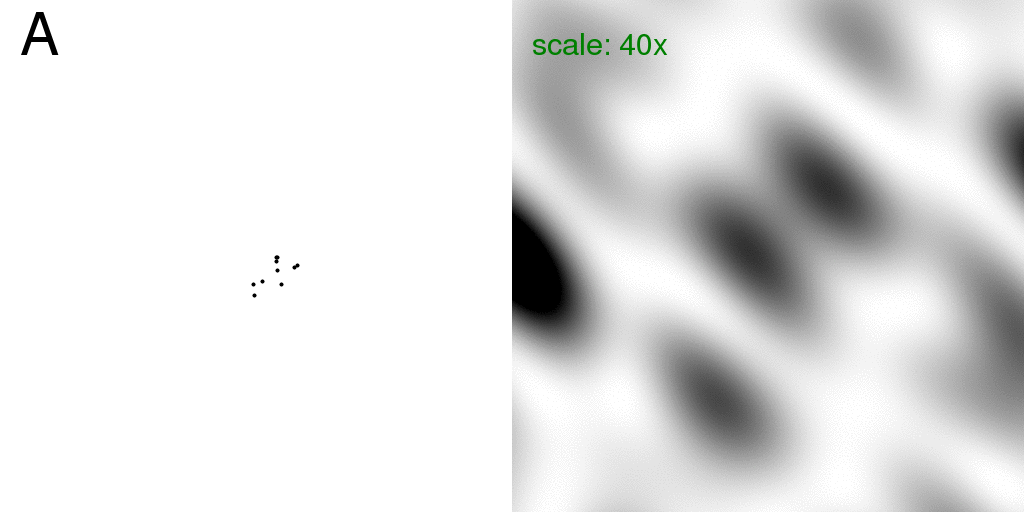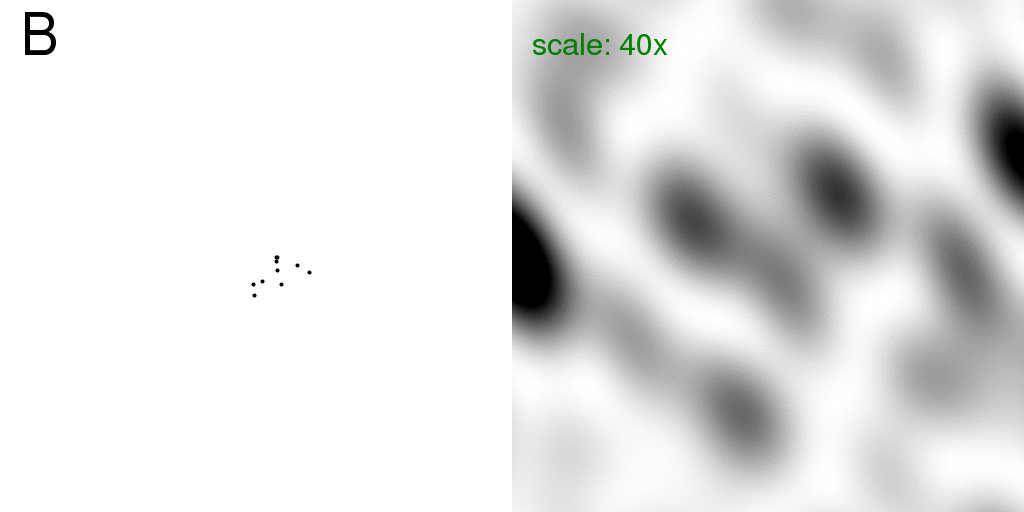
The green "scale:" text on the diffraction image indicates a number that the pixel intensities were multiplied by before converting them into the 8-bit image shown.
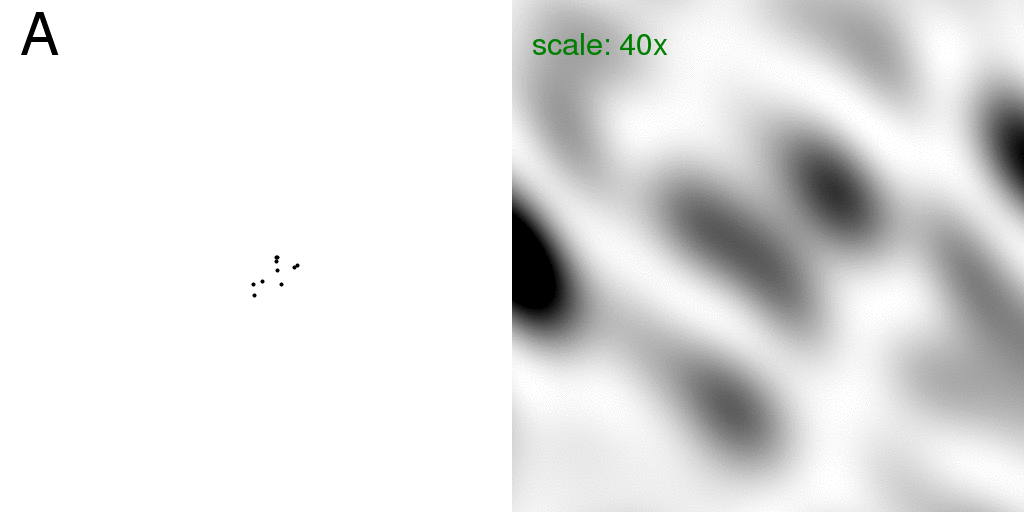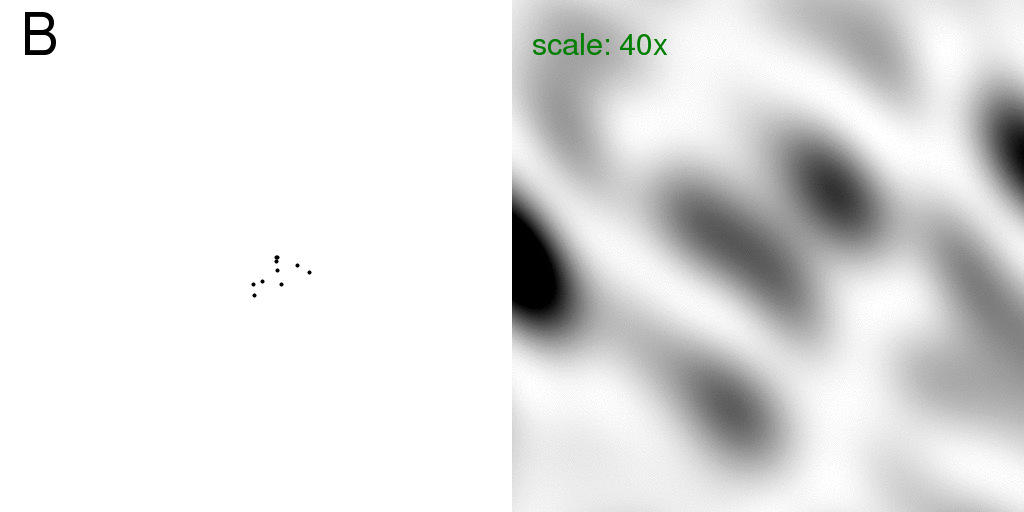
Now consider that one of these atoms is "floppy" in that it may occupy one of two possible positions (relative to the others). This means that 10% of the scattering matter is "disordered", and all other atoms in the structure are stable. This is analogous to a small protein with a two-headed side chain. That is, we have two structures: "A" and "B" which are identical except that our one floppy atom is in one position or the other.
Below, is a GIF animation cycling back and forth between these two structures
(on the left) and the corresponding diffraction pattern of each structure is on the right.
These diffraction patterns were computed with the program
nearBragg2D
using 1 Angstrom x-rays, and a 512x512-pixel detector of 200 micron pixels positioned
2 meters away from the sample. The beam center is hitting the left edge of each diffraction
pattern exactly halfway down the image.

The green "scale:" text on the diffraction image indicates a number that the pixel
intensities were multiplied by before converting them into the 8-bit image shown.
The real-space image on the right has a pixel size of 1 Angstrom. Although the "atoms" in the above image occupy more than one pixel, for simplicity (and computational speed) nearBragg2D models all atoms as infinitely sharp points, which is equivalent to setting the atomic structure factor to one for all resolutions. The diffraction pattern is in black and white because here we are simply plotting the intensity at each pixel (no phase information!). The diffraction pattern shown here is therefore the square of what is sometimes referred to as the "molecular transform" or the Fourier transform of a single unit cell, isolated in space. This molecular transform is "sampled" by the crystal lattice, which we will see below.
Note that we are also only considering two dimensions. The concepts laid out here apply equally well to 3D crystals, but it is easier to represent a 2D structure and diffraction pattern on a flat computer screen. For example, a 3D diffraction pattern would have to be rotated in an "oscillation" in order to get fully-recorded spot intensities, but for the 2D patterns used here, we only need a "still". Essentially, everything you see here could be a 3D structure and 3D diffraction pattern, but just viewed as a projection down the Z axis (I.E. the hk0 plane).
Now, if this molecule were in the unit cell of a crystal, we would traditionally model
the floppy atom as two half-occupancy atoms at either of the possible positions.
We will refer to this as a "pre-averaged" structure, shown here:
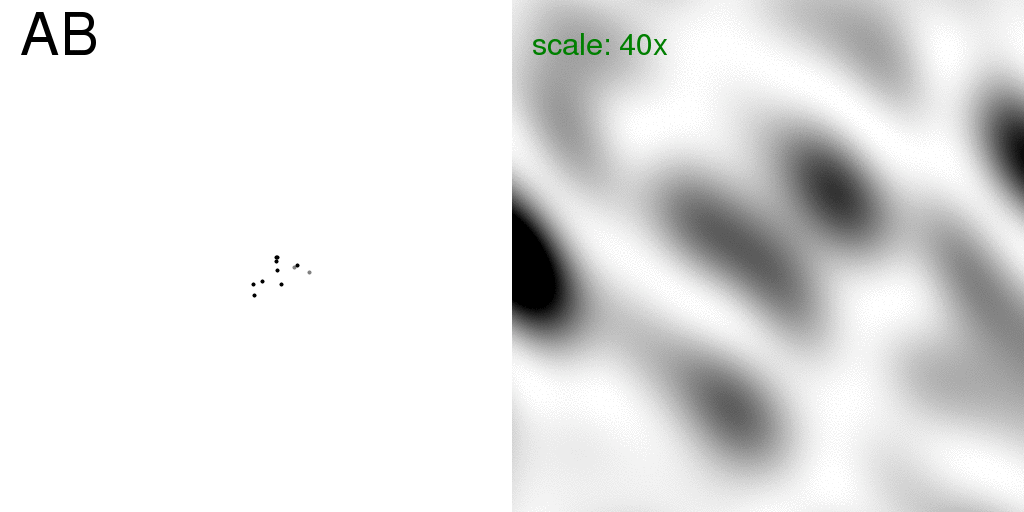
Note that the floppy atom is now colored grey to represent that it is only partially
occupying each position.
NB: the nearBragg program does not support occupancies on the atoms, but you can "hack" it by simply concatenating the atom lists and dividing the resulting intensity by four. That is, two atoms at exactly the same position will be equivalent to a single atom with twice the structure factor. Since the structure factor is squared to get intensity, you divide by four to normalize to the unit structure factor case (same scale as the last image).
However, if we were actually shooting a single molecule in our x-ray beam, the
floppy atom would
only be in one place or the other for each passing incident photon, and the diffraction
pattern we would actually see would simply be the sum of the intensities of the
diffraction pattern of each structure, taken separately. That is, we would just
see the sum of the two diffraction patterns being animated in Figure 1.
This intensity sum (divided by two) is shown below:
Here the real-space image (left) was set to rapidly animate the two structures back and
forth to emphasize
that the diffraction pattern on the right is the "average" diffraction, but without
considering the disordered atom to be at partial occupancy.
This is an example of the difference between
"coherent addition" (adding the Fs as vectors, and then squaring them) vs
"incoherent addition" (adding F2 or intensity).
Here we will call these the "F-sum" and "I-sum" images, respectively.
There is not that much
difference between them, since only 10% of the scattering matter is changing, but
there is a difference nonetheless. Mathematically, it is the cross-term from
squaring the complex structure factor, but the exact nature of the difference becomes
clear if you subtract the "F-sum" pattern from the "I-sum" pattern,
as shown here:

Since this is now a difference image, we have colored the atoms for the intensity sum
as red (positive) and the F-sum as blue (negative) since the F-sum image is being subtracted
from the I-sum image. Since nearly all the atoms overlap, the resulting color is magenta,
but you should hopefully be able to see a magenta atom flickering back and forth between
the faintly blue-colored partial-occupancy positions.
This representation emphasizes
that the I-sum image corresponds to the sum of diffraction events that occurred
separately (in time), but the F-sum image represents scattering off of a
pre-averaged structure (with partial occupancy atoms).
The difference is a series of diagonal bands because the floppy atom is moving 30 Angstrom to the right and 10 Angstrom down as it flips back and forth. That is, we are seeing the "negative" of the diffraction pattern of the disordered atom positions alone.
For comparison, here is the diffraction pattern of two (half-occupancy) atoms that
are the same distance
apart as the two possible positions of our disordered atom in the above structures:

Also, for completeness, these are the diffraction patterns for the individual atoms:

Note that the diffraction pattern of a single atom (isolated in space) is always
the same: no matter where it is! Therefore, the sum of the intensity from two atoms,
taken individually, is just twice the intensity of one. This is exactly how x-rays
scatter off of gas atoms. The scattering from a gas is simply the intensity scattered
from one particle, multiplied by the number of particles.
However, at this wavelength and detector distance the scattering from one point atom
is very flat. The image above was re-scaled and offset to show what little variation there is.
So, if we now subtract the I-sum image from the F-sum image (exactly as was done for
the whole structure above), we get the difference:

which is exactly the same as the difference seen in the context of the rest of the
structure.
To summarize, the difference between the I-sum diffraction pattern and the F-sum diffraction pattern is essentially the "negative" diffraction pattern of the disorder in the structure.
Now, let us consider packing this structure into a crystal!
Here, mainly for speed, we consider a crystal with only 9x9 unit cells and rounded
off to get a total of 69 lattice points. If we put just one atom in each unit cell,
we get the diffraction pattern of the lattice alone:

The red color in the diffraction pattern indicates "overloads" or pixels brighter than the
256 levels possible in this image. Here we have turned up the intensity scale so that
the "wiggles" around the Bragg peaks are visible. These wiggles arise because the
crystal has a finite size. In fact, the shape of each spot (including the wiggles) is
simply the Fourier transform of the shape of an envelope drawn around the crystal. In
this case, the crystal is round(ish) and so the spot shape is roughly an Airy disk.
It should be stressed here that
nearBragg2D
in no way considers unit cell dimensions or Airy disks or any such advanced concepts.
All the program does is add up the phases of scattered waves from each atom at each
detector pixel.
Now that we have a lattice, let us fill each unit cell with the "A" and "B" structures
discussed at the beginning. Below, we have filled the entire crystal with either all
"A"s or all "B"s. The resulting diffraction patterns are on the right:

Note that the diffraction pattern of the crystal is simply the molecular transform
(discussed above), multiplied by the structure factor of the lattice. This is because
a convolution in real space is a product in reciprocal space. However, we stress
again that
nearBragg2D
is in no way "aware" of these facts. It simply computes the total scattering from the
atoms provided. The program would be MUCH faster if it only calculated one unit cell
and the lattice separately and then multiplied the images together, but here we are
interested in diffuse scattering, so no such shortcuts have been taken.
So, just as with the single-molecule diffraction patterns above, we can generate the
diffraction pattern from the pre-averaged structure (with partial occupancy atoms in
grey):

or compute the all-A and all-B crystal diffraction patterns and average the intensities:

Again, what we see is the single-molecule diffraction pattern, multiplied by the lattice
pattern. The differences are subtle, but become more clear if we subtract the F-sum
image form the I-sum image (exactly as we did above):

One can see that the background between the spots shows some signs of the
diagonal-stripe difference signal we saw above.
But wait! Many (but not all) of the spot intensities are significantly higher in the I-sum image than the F-sum image! Does this mean that we are introducing huge errors in our Fcalcs by using partial-occupancy models? Possibly. The reason for this discrepancy is apparent if you look very closely at the animating atoms in the last two panels: they are all moving precisely in sync with one another. This is because our I-sum image is the sum of diffraction from two crystals with all unit cells in the same conformation. This is not an inconceivable situation in nature. Indeed a merohedrally twinned crystal is the I-sum of two different "conformations" where the conformations are a rotation of the entire unit cell.
However, in many cases (such as thermal vibration) there is little correlation from unit
cell to unit cell, and we will have a crystal where any given unit cell has a "probability"
of being conformer "A" or conformer "B". A few possibilities are animated here:

Note now that the floppy atoms are jumping around randomly. Only 10 possible structures
are shown above, but since there are 69 unit cells, there are a very large number of
combinations (269 = 6x1020)!
To model the true "diffuse scattering" from a crystal with unit cells equally likely
to be "A" or "B", we generated a total of 8192 different crystals, and averaged all the
intensities seen in their diffraction patterns:

At first glance, this diffraction pattern does not look all that different from the other
crystal diffraction patterns above, but if we subtract the F-sum image
(where every unit cell
has "A" and "B" at half occupancy each), we get the difference:

Here "overloaded" (too positive) pixels are colored red and negative peaks too large to
represent in this 8-bit image are colored blue. The intensity scale was turned WAY UP
in the above difference image so that the banded pattern of the difference structure
would show through. This is a very weak signal! But this is the "diffuse scattering"
intensity that must be measured in order to extract information about crystal disorder.
Note that many Bragg peaks have changed intensity, some positive and some negative.
This is because we only averaged 8192 diffraction patterns. As long as the arrangement
of unit cell types is random, these difference features at the Bragg peaks average out
to zero. To clarify this point, it is instructive to look at individual
randomly-arranged unit cell crystal diffraction patterns, with the F-sum image subtracted
from them:

Clearly, the Bragg peaks experience intensity fluctuations, but they appear equally
likely to be positive or negative for any given spot. Hence, after averaging millions
of patterns, one expects these fluctuations to average out.
It is instructive to consider what kind of relative error this might introduce in
Bragg peaks (the % difference). So, below each pixel of the animation above has
been divided by the average intensity of each pixel. The result has been scaled
so that each pixel level is 2% change in pixel intensity:

Also, one can look at the overall average percent difference between the above
8192-fold averaged diffuse scattering and the F-sum average:

In this case, one pixel level represents a 1% difference.
Clearly, there is some sort of pattern, but it is not the diagonal bands. Instead,
we are seeing the diagonal bands, divided by the molecular transform, which is much
more clear if we only consider single-particle diffraction:

Obviously, the percent difference becomes very large when the thing you are dividing by
gets very small. This is why all the "nodes" in the lattice diffraction pattern are
so clearly apparent. However, the percent change in spot intensities is always very
small, even when the molecular transform is weak.
It is perhaps interesting, however, that the fractional difference for a "synchronized"
crystal is exactly the same as that of an isolated structure:
Which has a mean value of about 12% in this case, but can range as high as a factor of two. RMS is 26%.
Dilatation:
Thus far, we have assumed that the crystal lattice itself is stable and imutable. But what
if the lattice is "bent" in some way? Wouldn't that make some "correlated disorder"
in the atom positions? What if there are other kinds of defects in the lattice?
The standard model for considering the effect of a defect on the rest of the crystal is
that of Kanzaki (1957).
In general, what happens is the rest of the unit cells are pushed or stretched by the
stress created by the defect, and the average unit cell expands a bit: a "dilatation".
Such increases in unit cell size are commonly seen in radiation damage studies, and, after
all, what is radiation damage if not the introduciton of a lot of randomly-placed changes in
unit cell contents? Evidence that protein crystals already have a lot of cell-dilatating
defects was found by Colin Nave (1998)
who showed that lysozyme crystals posess a range of unit cell sizes. What happens to the
areas "between" these cells? Well, the Kanzaki model would predict that the different
unit cell sizes occur within the same mosaic domain, and result in a pulling-and-stretching
effect:
Here I have used a simple-minded model that the displacement of an atom is simply given by
a Gaussian function centered on the defect. Each frame has one defect, placed randomly
in the field of view. This is equivalent to averaging over a lot of different regions of the
crystal with randomly-placed defects. The diffraction pattern is changed by these defects
and if we subtract the diffraction pattern of the partial-occupancy model:
we see that the spot intensities themselves are indeed affected by dilatation! The
difference is clearer if we look at the difference between the "Isum" diffraction pattern
and the "Fsum" diffraction pattern:
Note that this is not just the disorder in the atom positions (B factor) changing the
spot intensities, but an actual difference between the observed intensity (I-sum) and that
which would be predicted by a partial-occupancy model (F-sum). Note that the spots are
increasing in size radially, which is consistent with the spot shapes observed by
Nave (1998).
In this case, the maximum
atomic displacement is 5 Angstrom and we are looking at very low-angle spots
(10 Angstrom on the far right),
so the change in spot intensities is relatively small, but still remarkable. If we isolate
spot intensities with a filter, and look at the %-change in intensity,
we see that there is residual "extra intensity" under some
spots:
Here the scale has been multiplied by 20, so the red pixels indicate more than a 5% change
in intensity. The largest change in this image is 15%.
Conclusions:
Diffuse scattering is weak, but it does correspond to the "negative" of the intensity that
would be seen by all the disordered atoms in the crystal, taken by themselves.
As long as there are
no correlations between unit cells, the I-sum and F-sum Bragg intensities are identical
to a high degree of precision, and so there is nothing wrong with using partial-occupancy
models in crystallographic model refinement.
However, if the disorder is "synchronized" in some way across unit cells, then the "diffuse
scatter" intensity pattern migrates from in between the spots to influencing the
spots themselves! This does present problems for model refinement, as no single
"average electron density"
map will explain the diffraction pattern. That is, crystals with correlated
disorder will have some "twin character" and indeed merohedrally twinned crystals are
and extreme example of a crystal with two large regions dominated by different
molecular configurations.
Could this "correlated disorder" be responsible for why almost no protein crystal
R factors can be refined to below ~20%? Possibly, but the nature of the correlations
will need to be figured out before we can model it.
James Holton <JMHolton@lbl.gov>